Horizontal grit chamber: theory
How to verify the selected horizontal grit chambers with the storm sewer previously designed? To do this I have used my old notes of Hydraulic Constructions, topic of this article, and the relative BASIC software that I will publish soon, after I have checked and cleaned the code.
Theory
Pre-treatment may include a sand or grit channel or chamber, where the velocity of the incoming sewage is adjusted to allow the settlement of sand, grit, stones, and broken glass. These particles are removed because they may damage pumps and other equipment. For small sanitary sewer systems, the grit chambers may not be necessary, but grit removal is desirable at larger plants[1]. Grit chambers come in 3 types:
- horizontal grit chambers (see below);
- aerated grit chambers;
- vortex grit chambers.
Horizontal grit chamber
It is a particular basin posed along sewer system and accurately designed in length and area to assure the flow speed reduction at 0.30-0.50 m/s. The target of this type of chamber is allow at the sand particles (with a defined diameter) to be deposited to the bottom. This is due to the reduced flow speed and gravity.
In order to approximate this complex phenomenon there are two theories:
- elementary formulation (see below);
- Camp formulation.
Elementary formulation
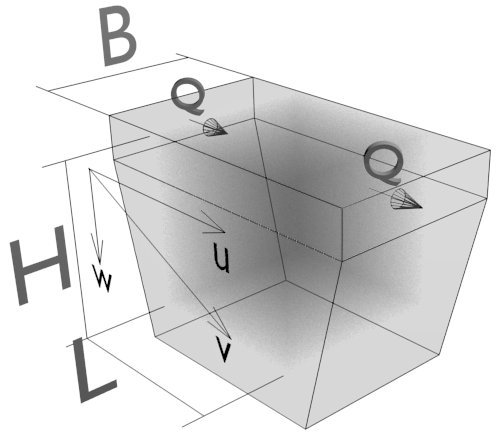 | Legend:
|
Firstly you have to verify the typical section of this chamber, because inside the useful sedimentation volume the average speed must be minor or equal than u=0.30-0.50 m/s. You can use this disequation:
\[ v_{in}= {Q \over A} < 0,3-0,5 m/s \]
Then you have to establish the specific weight and the minimal diameter of the sand particles that deposit in the bottom: Dmin, ?p.
The drop in speed in static water u can be calculated imposing the equilibrium between the weight force and dynamic resistance:
\[ (\gamma_p - \gamma_w) \cdot V_p = {{C_D \cdot A_p \cdot \rho_w \cdot w^2} \over {2}} \]
Where the letter p is an acronym of particle and ?, V, A are respectively its specific weight, volume and area.
After resolved the equilibrium equation, you find:
\[ w = \sqrt{{4 \cdot (\gamma_p - \gamma_w) \cdot D} \over {3 \cdot \rho_w \cdot C_D}} \]
Where:
γp= specific weight of the particle (25-26,5 kN/mc)
γw= specific weight of the water, 9,81 kN/mc
D = diameter of the particle
Ρw= unit of mass of the water, 1000 kg/mc
CD = coefficient of dynamic resistance.
This method is iterative: at the beginning the water flow is turbolent so you insert CD=0,4 until you reach the transition zone, where $C_D = 18,5 / {Re^{0,6}}= constant$. It follows the diagram between coefficient of dynamic resistance CD and Reynolds number $Re=\rho \cdot w \cdot D / \mu$.
| Laminar water flow | transition zone | turbulent water flow |
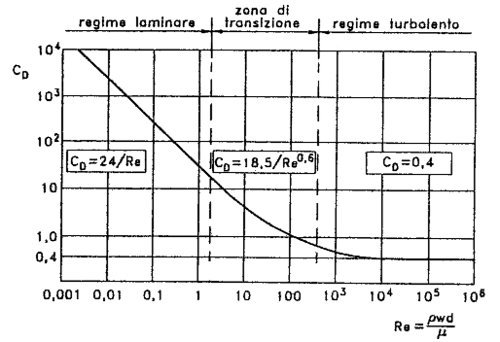 |
| Diagram between coefficient of dynamic resistance CD and Reynolds number |
After you have found w, drop in speed in static water, you can calculate the v speed, using:
\[ v = w - {{u} \over {5,7 + 2,3 \cdot H}} \]
Note: v is the speed for the selected particle, you should calculate w and v for a large range of diameters and weights (and their combinations!) and at the end choose the minimal speed. But you can find an approximate lenght L with:
\[ L \geq {{H \cdot u} \over {v}} \]
And then change it, comparing the drop time of the particle, t:
\[ t = {H \over v} \]
With time of distance covered in this useful sedimentation volume, t':
\[ t' = {L \over {Q \cdot A}} \]
L must ensure that $ t' \geq t$.
Finally the total length of this chamber Ltot must include the two zones with not-uniform speed (localized at the inlet and outlet of this grit trap):
\[ L_{tot} = L + 2 \cdot H/2 \]
References^
- [1 ] Sewage treatment on Wikipedia
- Luigi Da Deppo, Claudio Datei, Fognature, Padova, Cortina, 2002
- Relazione calcoli idraulici per il progetto e la verifica della rete pluviale di Terlizzi











Add new comment