About storm sewer design: an example
For developing the theory of linear reservoir model, I will try to design a small system shaped by 2 pipelines. In this example I show some useful table and I introduce the input data and calculations, in order to facilitate the comprehension and the using of my forthcoming FreeBASIC program.
Hydraulic question
It is required to design a storm sewer of a small residential area, its total surface is 1.10 ha (1 ha =104m2), and the distance between the A node to C is L=110 m. In the following scheme it is showed the area and two nodes. The surface is defined by heterogeneous parts with several permeability, but for brevity it uses only a mean permeability ratio in every surface.
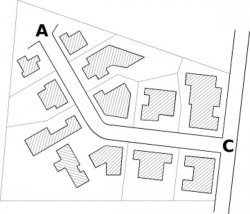
Schematization
Firstly it begins with a subdivision of the surface in single parts that compose the system. You have to ensure that between a upstream line and the next, the diameters should be exactly the following commercial diameter. To have an idea I put some data from this site: Oppo - il sito dell'impiantistica idraulica.
| 80 | 100 | 125 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 | 600 | 700 | 800 |
Generally the first open line diameter (A node) is sized following the prescribed regulations (in Italy the minimal diameter is fixed in 300 mm). The system is designed following the existent streets. Every line has a specific surface with an own average degree of permeability, calculated with this equation:
\[ \bar{\phi} = {{\sum \phi_i \cdot S_i} \over {\sum S_i}} \]
Where the single numerical values can be:
| Typology | $\phi$ |
| Impermeable surface (asphalt street, roof) | 0.90 |
| Semi-permeable (dirt floor) | 0.60 |
| Permeable surface (garden, tilled soil) | 0.20 |
Input data
The system to calculate:
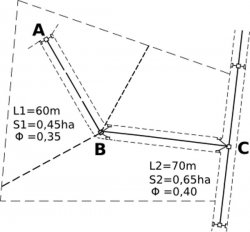
| Line | Surface | Length | $\phi$ | Diameter | Slope |
| - | ha | m | - | m | - |
| AB | 0.45 | 60 | 0.35 | 0.30 (assumptions) | 0.00322 |
| BC | 0.65 | 70 | 0.40 | ? | 0.00274 |
The area is limited so the time of concentration is expressed in minutes. I adopt the following local IFD curve (with Tr=10 years, typical for the sewers):
\[ h = a \cdot t^n = 51.4 \cdot t^{0.375} \]
For pipe type I assume that the Gauckler-Strickler roughness coefficient is $75 m^{1/3}/s$, here is it a table with many roughness coefficients. These pipes are shaped with a circular section so I use a table dimensionless calculated for this one. The table is designed beginning from filling degree (y/D) and the optimal ratio is between 0.75 and 0.85 y/D. It follows a reduced table (at the end I put the complete one).
| FILLING DEGREE | SURFACE | WET PERIMETER | HYDRAULIC RADIUS | MIRROR LIQUID LENGTH | BARYCENTER DEPTH | FLOW FACTOR | SPEED RATIO | FLOW RATIO |
| $y/D$ | $A/D^2$ | $P/D$ | $R_{H}/D$ | b/D | $z/D$ | ${A {R_{H}}^{2/3}} \over {D^{8/3}}$ | $v/v_0$ | $Q/Q_0$ |
| 0.01 | 0.0013 | 0.2003 | 0.0066 | 0.1990 | 0.0040 | 0.0000 | 0.0890 | 0.0002 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 1.00 | 0.7854 | 3.1416 | 0.2500 | 0.0000 | 0.5000 | 0.3117 | 0.3117 | 1.0000 |
Design
For linear reservoir model you have to use the following equations:
\[\begin{aligned} \epsilon &= 3.94 - 8.21 n + 6.23 n^2 \\ K_c &= \bigl({{10 \phi a} \over {3.6^n \epsilon}} \bigr)^{1 \over {1-n}} {{1} \over {ln{\epsilon \over {\epsilon - 1}}}} \\ u &= \Bigl( {K_c \over {v_0}}\Bigr)^{{1 - n} \over {n}} \\ Q &= u S \\ v_0 &= v_s + v_c\end{aligned} \]
The problem provides slopes, so you can use this variable to calculate the correct diameter, assuring an optimal filling degree.
AB line
| Line | Surface | Length | $\phi$ | Diameter | Slope |
| - | ha | m | - | m | - |
| AB | 0.45 | 60 | 0.35 | 0.30 (initial assumption) | 0.00322 |
$K_C$ is equal to 3662.411 and flow factor is:
\[ {{ {Q} \over {K_S \sqrt{i} } } \over {D^{8/3}}} = {{ {41.202} \over {75\sqrt{0.00322} } } \over {{0.30}^{8/3}}} = 0.24 \]
You have to look in table and check the corresponding y/D to the flow factor. In this case is 0.64 and go along until convergence. The following table is useful to clarify the operations:
| $v_0$ | $u$ | $Q=u \cdot S$ | $D$ | FLOW FACTOR | $y/D$ | $A/D^2$ | $v_{0B}={A \over D^2} \cdot D^2 \cdot L$ |
| m3/ha | l/s,ha | l/s | m | - | - | - | m3 |
| 40 | 91.56 | 41.202 | 0.3 | 0.24 | 0.64 | 0.53 | 2.86 |
| 46.36 | 78.99 | 35.55 | 0.3 | 0.207 | 0.60 | 0.49 | 2.65 |
| 45.88 | 79.83 | 35.92 | 0.3 | 0.209 | 0.60 | 0.49 | 2.65 |
The first value of $v_0$ is 40 m3/ha, the next ones are calculated by $v_s +v_{0B}/S_{AB}$, while $u$ and $Q$ are calculate by the standard formulas of this model.
Resulting for AB line:
\[\begin{aligned} Q &= 35.92\,l/s \\ D &= 0.3\, m \\ v &= 1.07\cdot v_0 = 1.07 [ 75 ( 0.2776 \cdot 0.3 )^{2/3} \cdot \sqrt{0.00322})] =0.868\,m/s \\ \tau &= \gamma R_H i = 9810 \cdot 0.2776 \cdot 0.3 \cdot0.00322 = 2.63\,N/m^2 \end{aligned} \]
BC line
| Line | Surface | Length | $\phi$ | Diameter | Slope |
| - | ha | m | - | m | - |
| BC | 0.65 | 70 | 0.40 | Ipotizzo 0.40 | 0.00274 |
$K_C$ is equal to 4783,557 and the calculations are:
| $v_0$ | $u$ | $Q=u \cdot S$ | $D$ | FLOW FACTOR | $y/D$ | $A/D^2$ | $v_{0C}={A \over D^2} \cdot D^2 \cdot L$ |
| m3/ha | l/s,ha | l/s | m | - | - | - | m3 |
| 44.1 | 119.589 | 77.73 | 0.4 | 0.2284 | 0.63 | 0.521 | 5.837 |
| 48.98 | 97.66 | 63.48 | 0.4 | 0.1865 | 0.57 | 0.4625 | 5.18 |
| 47.97 | 99.72 | 64.72 | 0.4 | 0.1904 | 0.60 | 0.49 | 5.18 |
In this case the first $v_0$ is a sum of $v_s +v_{0B}/S_{BC}$, instead the next ones are a sum of $v_s +v_{0C}/S_{BC}$, while $u$ and $Q$ are calculate by the standard formulas of this model.
Resulting for AB line:
\[\begin{aligned} Q &= 64.82\,l/s \\ D &= 0.4\, m \\ v &= 1.0533\cdot v_0 = 0.938\,m/s \\ \tau &= \gamma R_H i = 2.91\,N/m^2 \end{aligned}\]
Conclusions
If you use a ductile iron pipe, the line between A and B has to be divided again, because between AB and BC the variation of the diameters jumps the intermediate pipe diameter (the 350 mm model). Using cement pipe the assumptions are correct because the next pipe is a 400 mm model. If you found a filling degree bigger than 0.85, you would have to use a bigger diameter and update the calculations with this new diameter.
References:
- Luigi Da Deppo, Claudio Datei, Fognature, Padova, Cortina, 2002
- For technical tables: Oppo - il sito dell'impiantistica idraulica.
| FILLING DEGREE | SURFACE | WET PERIMETER | HYDRAULIC RADIUS | MIRROR LIQUID LENGTH | BARYCENTER DEPTH | FLOW FACTOR | SPEED RATIO | FLOW RATIO |
| $y/D$ | $A/D^2$ | $P/D$ | $R_{H}/D$ | b/D | $z/D$ | ${A {R_{H}}^{2/3}} \over {D^{8/3}}$ | $v/v_0$ | $Q/Q_0$ |
| 0.01 | 0.0013 | 0.2003 | 0.0066 | 0.1990 | 0.0040 | 0.0000 | 0.0890 | 0.0002 |
| 0.02 | 0.0037 | 0.2838 | 0.0132 | 0.2800 | 0.0080 | 0.0002 | 0.1408 | 0.0007 |
| 0.03 | 0.0069 | 0.3482 | 0.0197 | 0.3412 | 0.0120 | 0.0005 | 0.1839 | 0.0016 |
| 0.04 | 0.0105 | 0.4027 | 0.0262 | 0.3919 | 0.0161 | 0.0009 | 0.2221 | 0.0030 |
| 0.05 | 0.0147 | 0.4510 | 0.0326 | 0.4359 | 0.0201 | 0.0015 | 0.2569 | 0.0048 |
| 0.06 | 0.0192 | 0.4949 | 0.0389 | 0.4750 | 0.0241 | 0.0022 | 0.2892 | 0.0071 |
| 0.07 | 0.0242 | 0.5355 | 0.0451 | 0.5103 | 0.0282 | 0.0031 | 0.3194 | 0.0098 |
| 0.08 | 0.0294 | 0.5735 | 0.0513 | 0.5426 | 0.0322 | 0.0041 | 0.3480 | 0.0130 |
| 0.09 | 0.0350 | 0.6094 | 0.0575 | 0.5724 | 0.0363 | 0.0052 | 0.3752 | 0.0167 |
| 0.10 | 0.0409 | 0.6435 | 0.0635 | 0.6000 | 0.0404 | 0.0065 | 0.4012 | 0.0209 |
| 0.11 | 0.0470 | 0.6761 | 0.0695 | 0.6258 | 0.0444 | 0.0079 | 0.4260 | 0.0255 |
| 0.12 | 0.0534 | 0.7075 | 0.0755 | 0.6499 | 0.0485 | 0.0095 | 0.4500 | 0.0306 |
| 0.13 | 0.0600 | 0.7377 | 0.0813 | 0.6726 | 0.0526 | 0.0113 | 0.4730 | 0.0361 |
| 0.14 | 0.0668 | 0.7670 | 0.0871 | 0.6940 | 0.0567 | 0.0131 | 0.4953 | 0.0421 |
| 0.15 | 0.0739 | 0.7954 | 0.0929 | 0.7141 | 0.0608 | 0.0152 | 0.5168 | 0.0486 |
| 0.16 | 0.0811 | 0.8230 | 0.0986 | 0.7332 | 0.0650 | 0.0173 | 0.5376 | 0.0555 |
| 0.17 | 0.0885 | 0.8500 | 0.1042 | 0.7513 | 0.0691 | 0.0196 | 0.5578 | 0.0629 |
| 0.18 | 0.0961 | 0.8763 | 0.1097 | 0.7684 | 0.0732 | 0.0220 | 0.5775 | 0.0707 |
| 0.19 | 0.1039 | 0.9021 | 0.1152 | 0.7846 | 0.0774 | 0.0246 | 0.5965 | 0.0789 |
| 0.20 | 0.1118 | 0.9273 | 0.1206 | 0.8000 | 0.0816 | 0.0273 | 0.6151 | 0.0876 |
| 0.21 | 0.1199 | 0.9521 | 0.1259 | 0.8146 | 0.0857 | 0.0301 | 0.6331 | 0.0966 |
| 0.22 | 0.1281 | 0.9764 | 0.1312 | 0.8285 | 0.0899 | 0.0331 | 0.6507 | 0.1061 |
| 0.23 | 0.1365 | 1.0004 | 0.1364 | 0.8417 | 0.0941 | 0.0362 | 0.6678 | 0.1160 |
| 0.24 | 0.1449 | 1.0239 | 0.1416 | 0.8542 | 0.0983 | 0.0394 | 0.6844 | 0.1263 |
| 0.25 | 0.1535 | 1.0472 | 0.1466 | 0.8660 | 0.1025 | 0.0427 | 0.7007 | 0.1370 |
| 0.26 | 0.1623 | 1.0701 | 0.1516 | 0.8773 | 0.1067 | 0.0461 | 0.7165 | 0.1480 |
| 0.27 | 0.1711 | 1.0928 | 0.1566 | 0.8879 | 0.1110 | 0.0497 | 0.7320 | 0.1595 |
| 0.28 | 0.1800 | 1.1152 | 0.1614 | 0.8980 | 0.1152 | 0.0534 | 0.7471 | 0.1712 |
| 0.29 | 0.1890 | 1.1374 | 0.1662 | 0.9075 | 0.1195 | 0.0572 | 0.7618 | 0.1834 |
| 0.30 | 0.1982 | 1.1593 | 0.1709 | 0.9165 | 0.1237 | 0.0610 | 0.7761 | 0.1958 |
| 0.31 | 0.2074 | 1.1810 | 0.1756 | 0.9250 | 0.1280 | 0.0650 | 0.7902 | 0.2086 |
| 0.32 | 0.2167 | 1.2025 | 0.1802 | 0.9330 | 0.1323 | 0.0691 | 0.8038 | 0.2218 |
| 0.33 | 0.2260 | 1.2239 | 0.1847 | 0.9404 | 0.1366 | 0.0733 | 0.8172 | 0.2352 |
| 0.34 | 0.2355 | 1.2451 | 0.1891 | 0.9474 | 0.1410 | 0.0776 | 0.8302 | 0.2489 |
| 0.35 | 0.2450 | 1.2661 | 0.1935 | 0.9539 | 0.1453 | 0.0820 | 0.8430 | 0.2629 |
| 0.36 | 0.2546 | 1.2870 | 0.1978 | 0.9600 | 0.1496 | 0.0864 | 0.8554 | 0.2772 |
| 0.37 | 0.2642 | 1.3078 | 0.2020 | 0.9656 | 0.1540 | 0.0910 | 0.8675 | 0.2918 |
| 0.38 | 0.2739 | 1.3284 | 0.2062 | 0.9708 | 0.1584 | 0.0956 | 0.8794 | 0.3066 |
| 0.39 | 0.2836 | 1.3490 | 0.2102 | 0.9755 | 0.1628 | 0.1003 | 0.8909 | 0.3217 |
| 0.40 | 0.2934 | 1.3694 | 0.2142 | 0.9798 | 0.1672 | 0.1050 | 0.9022 | 0.3370 |
| 0.41 | 0.3032 | 1.3898 | 0.2182 | 0.9837 | 0.1716 | 0.1099 | 0.9132 | 0.3525 |
| 0.42 | 0.3130 | 1.4101 | 0.2220 | 0.9871 | 0.1760 | 0.1148 | 0.9239 | 0.3682 |
| 0.43 | 0.3229 | 1.4303 | 0.2258 | 0.9902 | 0.1805 | 0.1197 | 0.9343 | 0.3842 |
| 0.44 | 0.3328 | 1.4505 | 0.2295 | 0.9928 | 0.1850 | 0.1248 | 0.9445 | 0.4003 |
| 0.45 | 0.3428 | 1.4706 | 0.2331 | 0.9950 | 0.1895 | 0.1298 | 0.9544 | 0.4165 |
| 0.46 | 0.3527 | 1.4907 | 0.2366 | 0.9968 | 0.1940 | 0.1349 | 0.9640 | 0.4330 |
| 0.47 | 0.3627 | 1.5108 | 0.2401 | 0.9982 | 0.1985 | 0.1401 | 0.9734 | 0.4495 |
| 0.48 | 0.3727 | 1.5308 | 0.2435 | 0.9992 | 0.2031 | 0.1453 | 0.9825 | 0.4662 |
| 0.49 | 0.3827 | 1.5508 | 0.2468 | 0.9998 | 0.2076 | 0.1506 | 0.9914 | 0.4831 |
| 0.50 | 0.3927 | 1.5708 | 0.2500 | 1.0000 | 0.2122 | 0.1558 | 1.0000 | 0.5000 |
| 0.51 | 0.4027 | 1.5908 | 0.2531 | 0.9998 | 0.2168 | 0.1611 | 1.0084 | 0.5170 |
| 0.52 | 0.4127 | 1.6108 | 0.2562 | 0.9992 | 0.2214 | 0.1665 | 1.0165 | 0.5341 |
| 0.53 | 0.4227 | 1.6308 | 0.2592 | 0.9982 | 0.2261 | 0.1718 | 1.0243 | 0.5513 |
| 0.54 | 0.4327 | 1.6509 | 0.2621 | 0.9968 | 0.2308 | 0.1772 | 1.0319 | 0.5685 |
| 0.55 | 0.4426 | 1.6710 | 0.2649 | 0.9950 | 0.2355 | 0.1826 | 1.0393 | 0.5857 |
| 0.56 | 0.4526 | 1.6911 | 0.2676 | 0.9928 | 0.2402 | 0.1879 | 1.0464 | 0.6030 |
| 0.57 | 0.4625 | 1.7113 | 0.2703 | 0.9902 | 0.2449 | 0.1933 | 1.0533 | 0.6202 |
| 0.58 | 0.4724 | 1.7315 | 0.2728 | 0.9871 | 0.2497 | 0.1987 | 1.0599 | 0.6375 |
| 0.59 | 0.4822 | 1.7518 | 0.2753 | 0.9837 | 0.2545 | 0.2041 | 1.0663 | 0.6547 |
| 0.60 | 0.4920 | 1.7722 | 0.2776 | 0.9798 | 0.2593 | 0.2094 | 1.0724 | 0.6718 |
| 0.61 | 0.5018 | 1.7926 | 0.2799 | 0.9755 | 0.2642 | 0.2147 | 1.0783 | 0.6889 |
| 0.62 | 0.5115 | 1.8132 | 0.2821 | 0.9708 | 0.2690 | 0.2200 | 1.0839 | 0.7060 |
| 0.63 | 0.5212 | 1.8338 | 0.2842 | 0.9656 | 0.2739 | 0.2253 | 1.0893 | 0.7229 |
| 0.64 | 0.5308 | 1.8546 | 0.2862 | 0.9600 | 0.2789 | 0.2306 | 1.0944 | 0.7397 |
| 0.65 | 0.5404 | 1.8755 | 0.2881 | 0.9539 | 0.2839 | 0.2358 | 1.0993 | 0.7564 |
| 0.66 | 0.5499 | 1.8965 | 0.2900 | 0.9474 | 0.2889 | 0.2409 | 1.1039 | 0.7729 |
| 0.67 | 0.5594 | 1.9177 | 0.2917 | 0.9404 | 0.2939 | 0.2460 | 1.1083 | 0.7893 |
| 0.68 | 0.5687 | 1.9391 | 0.2933 | 0.9330 | 0.2990 | 0.2511 | 1.1124 | 0.8055 |
| 0.69 | 0.5780 | 1.9606 | 0.2948 | 0.9250 | 0.3041 | 0.2560 | 1.1162 | 0.8215 |
| 0.70 | 0.5872 | 1.9823 | 0.2962 | 0.9165 | 0.3093 | 0.2610 | 1.1198 | 0.8372 |
| 0.71 | 0.5964 | 2.0042 | 0.2975 | 0.9075 | 0.3144 | 0.2658 | 1.1231 | 0.8527 |
| 0.72 | 0.6054 | 2.0264 | 0.2987 | 0.8980 | 0.3197 | 0.2705 | 1.1261 | 0.8680 |
| 0.73 | 0.6143 | 2.0488 | 0.2998 | 0.8879 | 0.3250 | 0.2752 | 1.1288 | 0.8829 |
| 0.74 | 0.6231 | 2.0715 | 0.3008 | 0.8773 | 0.3303 | 0.2798 | 1.1313 | 0.8976 |
| 0.75 | 0.6319 | 2.0944 | 0.3017 | 0.8660 | 0.3357 | 0.2842 | 1.1335 | 0.9119 |
| 0.76 | 0.6405 | 2.1176 | 0.3024 | 0.8542 | 0.3411 | 0.2886 | 1.1353 | 0.9258 |
| 0.77 | 0.6489 | 2.1412 | 0.3031 | 0.8417 | 0.3466 | 0.2928 | 1.1369 | 0.9394 |
| 0.78 | 0.6573 | 2.1652 | 0.3036 | 0.8285 | 0.3521 | 0.2969 | 1.1382 | 0.9525 |
| 0.79 | 0.6655 | 2.1895 | 0.3039 | 0.8146 | 0.3577 | 0.3008 | 1.1391 | 0.9652 |
| 0.80 | 0.6736 | 2.2143 | 0.3042 | 0.8000 | 0.3633 | 0.3047 | 1.1397 | 0.9775 |
| 0.81 | 0.6815 | 2.2395 | 0.3043 | 0.7846 | 0.3691 | 0.3083 | 1.1400 | 0.9892 |
| 0.82 | 0.6893 | 2.2653 | 0.3043 | 0.7684 | 0.3748 | 0.3118 | 1.1399 | 1.0004 |
| 0.83 | 0.6969 | 2.2916 | 0.3041 | 0.7513 | 0.3807 | 0.3151 | 1.1395 | 1.0110 |
| 0.84 | 0.7043 | 2.3186 | 0.3038 | 0.7332 | 0.3866 | 0.3183 | 1.1387 | 1.0211 |
| 0.85 | 0.7115 | 2.3462 | 0.3033 | 0.7141 | 0.3927 | 0.3212 | 1.1374 | 1.0304 |
| 0.86 | 0.7186 | 2.3746 | 0.3026 | 0.6940 | 0.3988 | 0.3239 | 1.1358 | 1.0391 |
| 0.87 | 0.7254 | 2.4039 | 0.3018 | 0.6726 | 0.4050 | 0.3264 | 1.1337 | 1.0471 |
| 0.88 | 0.7320 | 2.4341 | 0.3007 | 0.6499 | 0.4113 | 0.3286 | 1.1311 | 1.0542 |
| 0.89 | 0.7384 | 2.4655 | 0.2995 | 0.6258 | 0.4177 | 0.3305 | 1.1280 | 1.0605 |
| 0.90 | 0.7445 | 2.4981 | 0.2980 | 0.6000 | 0.4242 | 0.3322 | 1.1243 | 1.0658 |
| 0.91 | 0.7504 | 2.5322 | 0.2963 | 0.5724 | 0.4308 | 0.3335 | 1.1200 | 1.0701 |
| 0.92 | 0.7560 | 2.5681 | 0.2944 | 0.5426 | 0.4376 | 0.3345 | 1.1151 | 1.0733 |
| 0.93 | 0.7612 | 2.6061 | 0.2921 | 0.5103 | 0.4445 | 0.3351 | 1.1093 | 1.0752 |
| 0.94 | 0.7662 | 2.6467 | 0.2895 | 0.4750 | 0.4517 | 0.3353 | 1.1027 | 1.0757 |
| 0.95 | 0.7707 | 2.6906 | 0.2865 | 0.4359 | 0.4590 | 0.3349 | 1.0950 | 1.0745 |
| 0.96 | 0.7749 | 2.7389 | 0.2829 | 0.3919 | 0.4665 | 0.3339 | 1.0859 | 1.0714 |
| 0.97 | 0.7785 | 2.7934 | 0.2787 | 0.3412 | 0.4743 | 0.3322 | 1.0751 | 1.0657 |
| 0.98 | 0.7816 | 2.8578 | 0.2735 | 0.2800 | 0.4823 | 0.3294 | 1.0618 | 1.0567 |
| 0.99 | 0.7841 | 2.9413 | 0.2666 | 0.1990 | 0.4908 | 0.3248 | 1.0437 | 1.0420 |
| 1.00 | 0.7854 | 3.1416 | 0.2500 | 0.0000 | 0.5000 | 0.3117 | 1.0000 | 1.0000 |














Add new comment